The first article in the Journal of Serendipitous and Unexpected Results (JSUR) has been published. Reminder: “JSUR is an open-access forum for researchers seeking to further scientific discovery by sharing surprising or unexpected results. These results should provide guidance toward the verification (or negation) of extant hypotheses.” (From the JSUR website.) I posted about JSUR before here and here.
And the article is pure blogging gold. But not in the sense you may think: it is actually very good. This is because it uses functional MRI (fMRI) on a dead salmon. Now why didn’t I think of that? So to explain what a dead salmon is doing in an MRI machine, I first have to explain the problem the DSIM (dead salmon in MRI) is solving.
Beware the FWER
Suppose you are flipping a coin, to test whether it is fair. The coin lands heads side up 9 times out of 10. So if you assume that the coin is fair, then the probability that a fair coin would come up heads at least 9 out of 10 times is (10 + 1) × (1/2)10 = 0.0107. This is relatively unlikely, and under statistical criteria such as p-value < 0.05, (meaing, your accepted error rate is 5%), you would declare that the the coin is unfair.
Now, suppose you flip 100 coins, 10 times each to test their fairness. Given that the probability of a fair coin coming up 9 or 10 heads in 10 flips is 0.0107, one would expect that in flipping 100 fair coins ten times each, to see any particular coin come up heads 9 or 10 times would still be very unlikely. But seeing some coin behave that way, without concern for which one, would be more likely than not. More specifically, the likelihood that all 100 fair coins are identified as fair by this criterion is (1 − 0.0107)100 ≈ 0.34. So there is a good chance that at least one coin will be falsely identified as unfair from 100 fair coins! This is because we are not dealing with one statistical test, but with a whole family of them. And we know how large families can be… Or rather, using the same significance criteria for a family of test that we use for a single test will bring up significant results where there are none.
So how do we solve this problem? Well, there are several ways. First, we have to determine the Familywise Error Rate (FWER) or False Discovery Rate, (FDR) which are two related measures used to estimate how much of such false-positive errors we are prone to make in any given family of tests. Then there are correction techniques we can apply, for example, the Bonferroni correction, which essentially divides the significance of “coming up heads” for each particular test by the number of tests. Using a much more rigid statistical threshold with Bonferroni correction with 100 (1 − 0.0107/100)100 ≈ 0.99. Therefore, the probability of any single outcome being classified as an unfair coin is now reduced to 0.01: much better.
(For you statistical purists out there: yes, this is not a rigorous explanation. I am trying to get the gist of it across).
This Fish has Ceased to Be
What has that got to do with fMRIs and a dead salmon?
fMRI tests are very popular. Why should they not be? Take someone, stick them in an MRI, show them a picture of their mother-in-law, see which bits of their brain light up (get more blood, hence are more active) and voila! You’re in the New York Times science supplement under the title “Scientists discover brain region responsible for unmitigated rage.” (Any resemblance to any actual mother-in-law, living or dead, is purely coincidental.) fMRI is a great tool for mapping cognitive processes into specific areas of the brain. It is our tool to connect between mind and brain, so to speak.
The pixels that appear in an fMRI scan are called voxels, or volume picture elements: fMRI scans provide brain slices that is reconstructed in 3D. A typical fMRI scan can contain 130,000 voxels. Tens of thousands of tests can be performed over multiple conditions. With the sheer number of images, can certain voxels light up as false-positives? You betcha. Is every voxel significant? Well, to answer that, Craig Bennett and his colleagues took a dead Atlantic Salmon, and placed it in an fMRI. The salmon was then shown a series of photographs depicting humans in various social situations. The (dead, remember?) fish was asked to determine which emotion each individual has been experiencing. They scanned the salmon’s (did I say it was dead?) brain, and collected the data. They also scanned the brain without showing the fish the pictures. The images were then checked for change between the brain doing picture recognition tasks, and the brain at rest, voxel by voxel. They found several active voxel clusters in the (yes, still dead) salmon’s brain. See below:
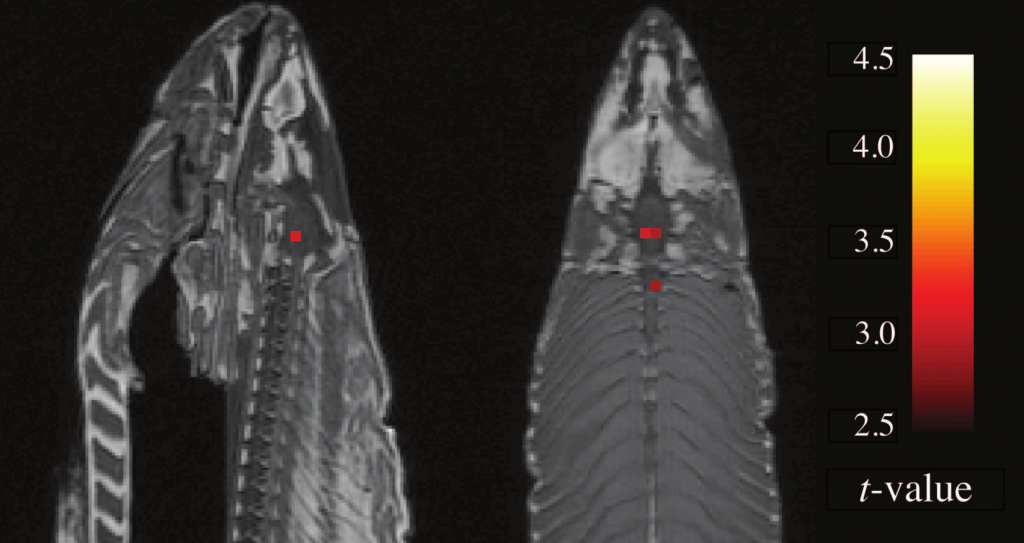
"Sagittal and axial images of significant brain voxels in the task > rest contrast. The parameters for this comparison were t(131) > 3.15, p(uncorrected) < 0.001, 3 voxel extent threshold. Two clusters were observed in the salmon central nervous system. One cluster was observed in the medial brain cavity and another was observed in the upper spinal column." (From Bennett et al 2010 JSUR 1:1 1-5)
So, what we have here is a very dead fish that can recognize emotions in humans? Not really: of course they will find some voxels out of the 130,000 lighting up! Just like you would have a good chance of finding any non-specific coin out of 100 falling heads-up 9 out of ten times. Of course, once they used corrections, the voxels were smoothed out.
My conclusion from this: awesome paper, showing us (1) how some serendipitous results should be interpreted: very carefully, with a grain of salt and with the proper FWER and FDR corrections for multiple pairwise tests. Serendipity might just be spurious, even if it does not seem to be. Also (2) know your statistics, or be a dead fish.
Golden quotes from the paper:
“It is not known if the salmon was male or female, but given the post-mortem state of the subject this was not thought to be a critical variable.”
“Either we have stumbled onto a rather amazing discovery in terms of post-mortem ichthyological cognition, or there is something a bit off with regard to our uncorrected statistical approach.”
Craig M. Bennett, Abigail A. Baird, Michael B. Miller, & George L. Wolford (2010). Neural Correlates of Interspecies Perspective Taking in the Post-Mortem Atlantic Salmon: An Argument For Proper Multiple Comparisons Correction JSUR, 1 (1), 1-5 Other: http://jsur.org/v1n1p1