When is it a good idea to cheat?
I have written before about bacterial cooperation, and how cheating works, up to a point, in an environment of bacterial cooperation. That post talked about bacterial quorum sensing, the collective signaling mechanism by which bacteria construct supra-cellular structures called biofilms. Biofilms are tough multicellular enclosures that allow bacteria to survive and thrive in hostile environments, and to invade host species. Both studies have shown that freeloading does not pay off. Bacteria who do not chip in to build the biofilm, yet benefit from it are ultimately doomed — and sometimes doom the collective of which they are constituents. That post dealt with the “here and now” aspect of cooperation and cheating.
This post deals with another aspect of bacterial cooperation: how does it evolve? Why cooperate in the first place at all? Every time an individual cooperates, short term gains are sacrificed for long-term ones, but those long-term ones are contingent upon all or most cooperating individuals doing their bit. Think about standing in line to the bus. If everyone cooperates, we get on the bus faster, but some of us may be forced to stand. On the other hand, shoving your way to the beginning of the line will assure you a good seat, albeit at the expense of glares from your fellow-passengers, and maybe a few altercations along the way. In evolutionary terms, selfishness seems like a sounder strategy than cooperating. After all, if you manage to gain a better position for yourself in life’s pecking order, you pass those genes that enable that to your progeny, and further down the line. Why cooperate or act selflessly in the first place? Why let someone else share the gene pool with you when you can have it all to yourself?
![]()
Unless that “someone else” shared genes with you: that is, they were related in some way. Suddenly, cooperation seems to have evolutionary benefits: you are preserving and passing on some of the same genes. Protecting kin is the most often-used explanation for how cooperation evolved in the first place: kin selection, meaning, favoring cooperation those individuals with which you share a larger number of genes over those who do not. Evolutionary biologists use the Hamilton’s law as a guideline: the higher the benefit of the cooperation, the lower the cost, and the closer the relatedness of the individuals cooperating, the more likely it is that there will be cooperation. Putting it into an equation, cooperation will evolve if the following condition is met:
rb - c > 0
Where r is the relatedness (on a scale of 0 to 1 where 0: no genetic relation, 1:self), b is the benefit of cooperation and c is the cost. This rule, formulated by William Donald Hamilton is a centerpiece of evolutionary biology. Imagine going on a day’s hunt where the quarry is a large animal that can feed one hunter for 35 days, but requires at least five hunters to take it down. Now there are also smaller animals around, that can be hunted by one individual, and they supply enough food for one hunter for two days. Is it beneficial to hunt alone or together? Let’s figure the benefits and costs. For hunting the large animal, the one that requires at least five hunters, the benefit is a week of food each (b= 35/5 = 7) while hunting for one day (c=1). If the individuals are cousins sharing an average of 20% of the genetic material then:
0.2×7 – 1 = 0.4 is the benefit score
If they are siblings, sharing 50% of the genetic material, then:
0.5×7 – 1 = 2.5 the benefit score is even higher
But what about individual hunting? The benefit of the smaller quarry is is 2 days worth of food, and one day of hunting, and you do it alone. So r=1 (yourself), b=2 and c=1 giving us:
1×2-1 = 1
In this hypothetical model, a group of siblings will cooperate to hunt big game, while cousins would probably hunt smaller game alone. If you want to dig deeper into how Hamilton’s rule was derived, and further implications of the rule, I recommend this post.
Any mechanism in evolution is examined through the lens of fitness. Fitness is the relative ability to produce and support viable progeny. So if cooperation increases fitness, we can use the following simple graph to explain the difference between a cooperating and a non-cooperating individuals in a cooperating population using Hamilton’s rule:
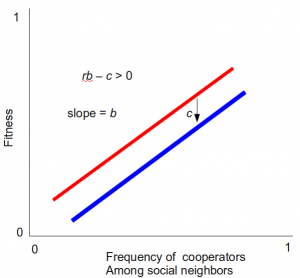
Figure 1: Hamilton's rule prediction: the fitness of cooperators (blue) and non-cooperators (red) increases as the number of cooperators among social neighbors (x-axis) increases. The slope of both lines is the benefit (b).
The benefit, b, is the slope of these two lines. The difference is c. Note that for any given frequency of cooperation in the population, the non-cooperating individuals (red line) have a higher fitness than the cooperating ones (blue line). It seems that it “pays off” to be a self-server no matter the social environment you are in, even though you still benefit from being in a cooperating community. Yeah, we all know the type.
But what happens when the difference between cooperating and not cooperating depends on the percentage of cooperators in the population? Not too hard to imagine: if most of the population is playing nicely together and benefiting from it, then this might change the attitude of the selfish individuals more readily then if only a small fraction of the population is cooperating. But as it stands, Hamilton’s rule does not provide for this type of model. However, the following modification of Hamilton’s rule does:
r ⋅ b – c + m ⋅ d > 0
Relatedness, r, is now not a scalar (a single number), but a vector (an ordered set of values) r = {r1, r2, …} describing relatedness under different conditions. Ditto the benefit vector, b. b has the coefficients of the equation describing the fitness of non-cooperators as a function of how many neighboring cooperators there are in the population (red lines). In a linear setting (Figure 1), r = {r1} b={b1} and m⋅d = 0, collapsing the expanded equation into the classical Hamilton’s rule. We won’t get into m and d in this post, they are important though, and you should read the paper to understand how they play a role
Expanding them from scalars to vectors enables a richer and more flexible description of Hamilton’s rule, allowing to describe non-linear relationships like this:
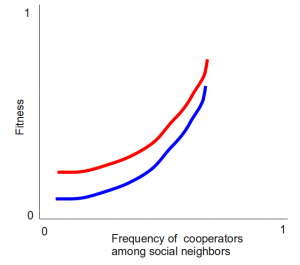
Figure 2: Note two things. First, the relationship between fitness and the fraction of cooperators in the population is not linear. Second, the difference in fitness between cooperators and non-cooperators decreases as the fraction of cooperators in the population goes up. These two phenomena cannot be described by the classic Hamilton's rule equation. They can be described using the modified rule.
This modification of Hamilton’s rule was developed by Jeff Smith and colleagues, at the department of Biology at Indiana University. Armed with the new equation, Smith and his colleagues decided to see how well it can be applied. They decided to look at Myxococcus xanthus. M. xanthus bacteria behave normally as long as food is abundant: they swim around and proliferate by cell-division as bacteria do. But when starved, they aggregate, and some cells form resistant spores, while the others die. Some cheating strains sporulate well when in cooperating populations, but do poorly on their own. The scientists mixed a cooperator strain with a cheating strain at different frequencies, starved them, and measured the fraction of each strain in the population of surviving spores. They found the following: first, the fitness effect was non-linear; in fact, it was almost exponential. Second, cooperators were more fit than cheaters at low cooperator frequencies, but cheaters fared better at high cooperator frequencies. So it pays to freeload when most people around you behave nicely. In the case of M. xanthus, the added value to the population is quite high. In fact, the scientists found that cooperation in M. xanthus is very robust and resistant to cheating: cheaters were viable (i.e. had a positive fitness) only with groups that had more than 70% cooperators. So it is only when cheaters have a large cooperating population to buffer their nasty habits that a they can thrive.
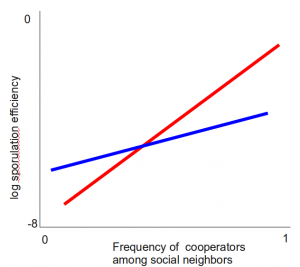
Figure 3: Relative fitness of cooperators (blue) and cheaters (red) in a populations with different relative frequencies of cooperators. Note that the fitness scale is logarithmic: the fitness increase is very much non-linear, as in Figure 2.
Moral of this story: if you got to cheat, make sure there are a lot of nice people around. Otherwise it won’t work out very well. In evolutionary terms, the trait for cooperation and kin selection has evolved to become strongly entrenched, so much that cheaters can only survive if cushioned by a high frequency of cooperators. Favoring your own and acting selflessly towards them seems to be the way to go, in the case of M. xanthus.
smith, J., Van Dyken, J., & Zee, P. (2010). A Generalization of Hamilton’s Rule for the Evolution of Microbial Cooperation Science, 328 (5986), 1700-1703 DOI: 10.1126/science.1189675



















Nice article. A further comment on evolving cooperation: In order to explain emergence of cooperation in this context, you don’t necessarily need kin selection. If you assume that, supported by geometric issues, different groups of various bacteria form, those groups with a healthy preference towards cooperation will grow faster and overtake areas with selfish, and therefore less performant mixtures.
Perhaps I’m just not understanding something, but Hamilton’s Law appears to be missing out on a rather important parameter: the value to me of the cooperation.
Take your hunting example. If I join with 4 other people and hunt big game, then in 1 day I get 7 days worth of food. If I hunt small game on my own, I get 2 days worth of food.
Therefore, unless I expect the other 4 to gang up and steal all the food, the benefit to me is 6, even if I’m totally unrelated to the other hunters. Which means I’m going to hunt big game with anyone who I think won’t rob me.
No?
@Greg D
You are actually taking one parameter out of Hamilton’s equation. In your case it is b-c > 0. It’s true that you benefit from hunting with anyone who will not rob you. But from a gene-centric view of evolution, the ones you can “trust” are the ones sharing genes with you, the more shared genes the better. Therefore, factoring b by r tells you how much fitness is gained, which, from a gene-centric view is the capability of proliferating the maximal number of genes. The entity that stands to benefit is not a single organism, (e.g. Greg) but for the pool of genes Greg has, and shares with his kin.